Introduction to Deep Learning - Part 2
Deep Q-Learning
Context
This session is an introduction to Reinforcement Learning, and more particularly Deep Q-Learning. Some parts of this course, as well as code snippets, are reproduced from this great Pytorch Tutorial
Installation
We will be coding with Python3 and will use the Pytorch and gym libraries.
To install Pytorch on your local machine, follow this link.
To install gym, simply run pip install gym
The Cartpole task
In the Gym Cartpole task, an agent must decide between two actions, i.e. moving the cart to the left or the right, so that the attached pole stays upright. The episode ends when the pole is more than 15 degrees from vertical, or the cart moves more than 2.4 units from the center.
The first step is to create a gym environment.
import gym
env = gym.make('CartPole-v0').unwrapped
With the following code, you can visualize a random agent. You will notice that episodes obviously end very quickly.
num_episodes = 10
for _ in range(num_episodes):
# Reset environment
initial = env.reset()
done = False
while not done:
env.render()
random_action = env.action_space.sample()
observation, reward, done, info = env.step(random_action)
Basics
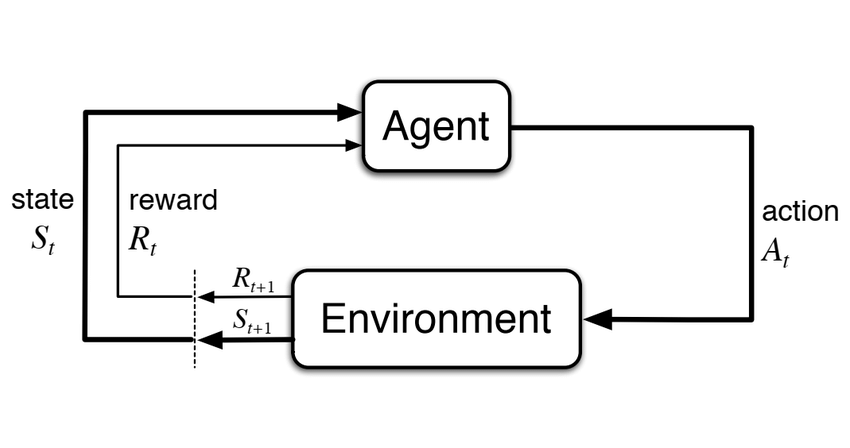
You have covered the fundamentals of Reinforcement Learning (RL) and Q-Learning in your last lecture.
Markov Decision Process (MDP)
Any RL problem can be formulated as a Markov Decision Process (MDP) characterised by:
- Set of states $S$
- Set of actions $A$
- Transition function $P(s_{t+1} \mid s_t, a_t)$
- Reward function $R(s_t, a_t, s_{t+1})$
- Start state $s_0$
- Discount factor $\gamma$
- Horizon $H$
A trajectory $\tau$ is a sequence of states and actions,
\[\tau = (s_0, a_0, s_1, a_1, ..., s_H)\]We can then define the return $R(\tau)$ as follows,
\[R(\tau)=\sum_{t=0}^{H} \gamma^{t} r_{t}\]The goal is to find the policy $\pi$ maximizing the expected return $J(\pi)$ defined as,
\[J(\pi)=\underset{\tau \sim \pi}{\mathrm{E}}[R(\tau)]\]Q-Value
The optimal Q-Value $Q^*(s, a)$ is the expected return when starting in state $s$, taking action $a$ and then acting optimally until the end of the episode. The optimal Q-Value can be defined recursively through the Bellman Equation,
\[Q^{*}(s, a)=\sum_{s^{\prime}} P\left(s^{\prime} \mid s, a\right)\left(R\left(s, a, s^{\prime}\right)+\gamma \max _{a^{\prime}} Q^{*}\left(s^{\prime}, a^{\prime}\right)\right)\]Tabular Q-Value iteration
When knowing the dynamics of the environment (i.e. $P(s_{t+1} \mid s_t, a_t)$), the optimal policy $\pi^*$ can be found using exact methods such as Q-Value iteration or Policy Iteration. The update rule, repeated until convergence, of the tabular Q-Value iteration algorithm is as follows,
\[Q_{k+1}(s, a) \leftarrow \sum_{s^{\prime}} P\left(s^{\prime} \mid s, a\right)\left(R\left(s, a, s^{\prime}\right)+\gamma \max _{a^{\prime}} Q_{k}\left(s^{\prime}, a^{\prime}\right)\right)\]Tabular Q-Learning
However, in most interesting problems, such dynamics are unknown. The previous expression can be re-written as an expectation,
\[Q_{k+1}(s, a) \leftarrow \mathbb{E}_{s^{\prime} \sim P\left(s^{\prime} \mid s, a\right)}\left[R\left(s, a, s^{\prime}\right)+\gamma \max _{a^{\prime}} Q_{k}\left(s^{\prime}, a^{\prime}\right)\right]\]This expectation can be approximated by sampling. An agent can thus collect samples so that we can approximate $Q_{k+1}(s, a)$ instead of computing it exactly. Given a new collected sample state $s^{\prime}$, the Q-Learning update equation becomes,
\[Q_{k+1}(s, a) \leftarrow(1-\alpha) Q_{k}(s, a)+\alpha\left[R\left(s, a, s^{\prime}\right)+\gamma \max _{a^{\prime}} Q_{k}\left(s^{\prime}, a^{\prime}\right)\right]\]Deep Q-Learning
In tabular Q-Learning, we need to keep track of a Q-value for each pair $(s, a)$. However, as problems become more realistic, and thus interesting, this becomes intractable. The idea is to have, instead of a table, a parametrized Q-function $Q_\theta(s, a)$.
In the case of Deep Q-Learning, this function will be a neural network. The update rule will not be about updating the entry corresponding to the $(s, a)$ pair in a table as it was done in previous euqations, but to update the weights $\theta$ of the neural network,
\[\theta_{k+1} \leftarrow \theta_{k}-\left.\alpha \nabla_{\theta}\left[\frac{1}{2}\left(Q_{\theta}(s, a)-\left[R\left(s, a, s^{\prime}\right)+\gamma \max _{a^{\prime}} Q_{\theta_{k}}\left(s^{\prime}, a^{\prime}\right)\right]\right)^{2}\right]\right|_{\theta=\theta_{k}}\]Deep Q-Network (DQN)
Now that we have reviewed some theory, let’s start practicing!
Implement a Deep Q-Network that takes as input the current state $s_t$ and outputs $Q_\theta(s_t, a)$ for each available action $a$. Be careful of the dimensions of the observation tensor that will be fed to your network, and think about the desired output dimension. As a sanity check, verify you can pass it one observation from your gym environment.
DQN Training
Setting up training
You must fill in the following code. Different parts are annotated. Refer to the following subsections for more details.
# Create the environment
env = gym.make('CartPole-v0').unwrapped
# Set up matplotlib
is_ipython = 'inline' in matplotlib.get_backend()
if is_ipython:
from IPython import display
plt.ion()
# If gpu is to be used
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# Reset the environment
env.reset()
# Useful hyperparameters (try to play with them)
EPISODES = 200 # number of episodes
EPS_START = 0.9 # e-greedy threshold start value
EPS_END = 0.05 # e-greedy threshold end value
EPS_DECAY = 200 # e-greedy threshold decay
GAMMA = 0.8 # Q-learning discount factor
LR = 0.001 # NN optimizer learning rate
HIDDEN_LAYER = 256 # NN hidden layer size
BATCH_SIZE = 64 # Q-learning batch size
TARGET_UPDATE = 10 # Update frequency of the target network
# Get number of actions from gym action space
n_actions = env.action_space.n
##############################################
# 1. Instantiate your DQN and the target network
##############################################
##############################################
# 2. Create your replay memory
##############################################
##############################################
# 3. Choose and instantiate your optimizer
##############################################
# Count steps and episode durations
steps_done = 0
episode_durations = []
1. Target Network
Deep Q-Learning can be quite unstable. Thus, a trick is to instantiate one DQN, and another copy of the same model, known as target network. The parameters of the latter will be updated every $n$ steps to match the parameters of the DQN you optimize. The target network is used to compute the target Q-value in the update rule.
2. Replay Buffer
In RL, as training data is collected while interacting with the environment, samples are correlated. The fundamental assumption of i.i.d (idependently and identically distributed) samples is thus violated.
In order to get more decorrelated samples, an adopted solution is to rely on a replay memory where observations are stored while interacting to be re-used later during training. This has been shown to stabilize training and improve the downstream performance of DQN agents.
You can use the following python class from the PyTorch Tutorial
from collections import namedtuple, deque
Transition = namedtuple('Transition',
('state', 'action', 'next_state', 'reward'))
class ReplayMemory(object):
def __init__(self, capacity):
self.memory = deque([],maxlen=capacity)
def push(self, *args):
"""Save a transition"""
self.memory.append(Transition(*args))
def sample(self, batch_size):
return random.sample(self.memory, batch_size)
def __len__(self):
return len(self.memory)
3. Optimizer
In the original paper introducing DQN to play Atari Games, authors chose to use the RMSProp optimizer. You should start by trying the same as well.
Acting in the environment
Our agent must take actions in the environment. As a common practice, we will adopt the $\epsilon$-greedy approach, where we select a random action with probability $\epsilon$, and otherwise the action $a$ with highest Q-value when being in state $s_t$ according to our DQN.
Implement the following function to take actions,
def select_action(state):
global steps_done
steps_done += 1
##############################################
# Random action with proba epsilon and argmax DQN(s,a) otherwise
##############################################
Optimizing our DQN
You must now fill in the function that takes care of optimizing the network.
def optimize_model():
if len(memory) < BATCH_SIZE:
return
transitions = memory.sample(BATCH_SIZE)
# Transpose the batch (see https://stackoverflow.com/a/19343/3343043 for
# detailed explanation). This converts batch-array of Transitions
# to Transition of batch-arrays.
batch = Transition(*zip(*transitions))
# Compute a mask of non-final states and concatenate the batch elements
# (a final state would've been the one after which simulation ended)
non_final_mask = torch.tensor(tuple(map(lambda s: s is not None,
batch.next_state)), device=device, dtype=torch.bool)
non_final_next_states = torch.cat([s for s in batch.next_state
if s is not None])
state_batch = torch.cat(batch.state)
action_batch = torch.cat(batch.action)
reward_batch = torch.cat(batch.reward)
##############################################
# Compute Q(s_t, a) from your DQN model
# state_action_values = ...
##############################################
##############################################
# Compute the target for your loss (that you will compare to state_action_values)
# expected_state_action_values = ...
##############################################
##############################################
# Compute Huber loss
# criterion = ...
# loss = ...
##############################################
# Optimize the model
optimizer.zero_grad()
loss.backward()
for param in policy_net.parameters():
param.grad.data.clamp_(-1, 1)
optimizer.step()
Huber Loss
In the original paper introducing DQN to play Atari Games, authors chose to use the Huber Loss. Try to do the same. Note that another name for such loss is SmoothL1Loss.
Training loop
You can now use the following training code and start optimizing your agent.
def plot_durations():
plt.figure(2)
plt.clf()
durations_t = torch.tensor(episode_durations, dtype=torch.float)
plt.title('Training...')
plt.xlabel('Episode')
plt.ylabel('Duration')
plt.plot(durations_t.numpy())
# Take 100 episode averages and plot them too
if len(durations_t) >= 100:
means = durations_t.unfold(0, 100, 1).mean(1).view(-1)
means = torch.cat((torch.zeros(99), means))
plt.plot(means.numpy())
plt.pause(0.001) # pause a bit so that plots are updated
if is_ipython:
display.clear_output(wait=True)
display.display(plt.gcf())
for i_episode in range(EPISODES):
# Initialize the environment and state
state = env.reset()
state = torch.from_numpy(state).unsqueeze(0).to(device)
for t in count():
env.render()
# Select and perform an action
action = select_action(state)
n_state, reward, done, _ = env.step(action.item())
reward = torch.tensor([reward], device=device)
# Observe new state
if not done:
next_state = torch.from_numpy(n_state).unsqueeze(0).to(device)
else:
next_state = None
# Store the transition in memory
memory.push(state, action, next_state, reward)
# Move to the next state
state = next_state
# Perform one step of the optimization (on the policy network)
optimize_model()
if done:
episode_durations.append(t + 1)
plot_durations()
break
# Update the target network, copying all weights and biases in DQN
if i_episode % TARGET_UPDATE == 0:
target_net.load_state_dict(policy_net.state_dict())
print('Complete')
env.render()
env.close()
plt.ioff()
plt.show()
Cartpole with screen images as input
If you have time, you can try to solve the cartpole problem, without relying on the state of the cartpole, but rather the image on the screen. This will mainly involve implementing a Convolutional DQN, and maybe playing with some of the hyperparameters…