Multi-Object Navigation with dynamically learned neural implicit representations

ICCV 2023

Paper Code ICCV 2023 poster ICCV 2023 video

Abstract

Understanding and mapping a new environment are core abilities of any autonomously navigating agent. While classical robotics usually estimates maps in a stand-alone manner with SLAM variants, which maintain a topological or metric representation, end-to-end learning of navigation keeps some form of memory in a neural network. Networks are typically imbued with inductive biases, which can range from vectorial representations to birds-eye metric tensors or topological structures. In this work, we propose to structure neural networks with two neural implicit representations, which are learned dynamically during each episode and map the content of the scene: (i) the Semantic Finder predicts the position of a previously seen queried object; (ii) the Occupancy and Exploration Implicit Representation encapsulates information about explored area and obstacles, and is queried with a novel global read mechanism which directly maps from function space to a usable embedding space. Both representations are leveraged by an agent trained with Reinforcement Learning (RL) and learned online during each episode. We evaluate the agent on Multi-Object Navigation and show the high impact of using neural implicit representations as a memory source.

Multi-ON

We target the Multi-ON task, where an agent is required to reach a sequence of target objects, more precisely coloured cylinders, in a certain order, and which was used for a recent challenge organized in the context of the CVPR 2021 Embodied AI Workshop. Compared to much easier tasks like PointGoal or (Single) Object Navigation, Multi-ON requires more difficult reasoning capacities, in particular mapping the position of an object once it has been seen. The following capacities are necessary to ensure optimal performance: (i) mapping the object, i.e. storing it in a suitable latent memory representation; (ii) retrieving this location on request and using it for navigation and planning, including deciding when to retrieve this information, i.e. solving a correspondence problem between sub-goals and memory representation. The agent deals with sequences of objects that are randomly placed in the environment. At each time step, it only knows the class of the next target, which is updated when reached. The episode lasts until either the agent has found all objects in the correct order or the time limit is reached.

Baselines

Multi-ON baselines (NoMap, ProjNeuralMap, OracleMap, OracleEgoMap) are presented here

Dynamic Implicit Representations

The Semantic Finder \(f_s\)

The aim of this model is to localize an object of interest within the scene. From a query vector given as input, the Semantic Finder predicts the position of the object, which is particularly useful for an agent interacting with an environment in the context of a goal conditioned task. It is implemented as a 3-layer MLP with ReLu activations in the intermediate layers and a sigmoid activation for the output. Hidden layers have 512 neurons. The query vector q corresponds to the 1-in-K encoding of the target object class, which during navigation is directly determined by the object goal gt provided by the task

The Occupancy and Exploration Implicit Representation \(f_o\)

Unlike \(f_s\), the occupancy representation \(f_o\) is closer to classical implicit representations in robotics, which map spatial coordinates to variables encoding information on navigable area like occupancy or signed distances. Different to previous work, our representation also includes exploration information, which changes over time during the episode. Once explored, a position changes its class, which makes our neural field dynamic. Another difference with \(f_s\) is that the latter deals with 3D coordinates while \(f_o\) is a topdown 2D representation. Inspired by previous work, the model uses Fourier features extracted from the 2D coordinates x previously normalized \(\in [0, 1]\). The network fo is a 3-layer MLP with ReLu intermediate activations and a softmax function at the output layer. Hidden layers have 512 neurons.

The Global Reader \(r\)

The Occupancy and Exploration Representation can in principle be queried directly for a single position, but reading out information over a large area directly this way would require multiple reads. We propose to compress this procedure by providing a trainable global read operation \(r(.; \theta_g)\), which predicts an embedding e containing a global context about what has already been explored, and positions of navigable space. The prediction is done directly from the trainable parameters of the implicit representation, as \(e = r(\theta_o; \theta_r)\). Here \(\theta_o\) is input to \(r\), whereas \(\theta_r\) are its parameters.

The Global Reader is implemented as a transformer model with self-attention. It takes as input a sequence of tokens \((w_1, ..., w_N )\), where \(w_i \in R^a\) is a learned linear embedding of the incoming weights of one neuron within the implicit representation \(f_o\), and \(N\) is the number of neurons of \(f_o\). Each token is summed with a positional encoding in the form of Fourier features. An additional “CLS” token with learned embedding is concatenated to the input sequence. The reader is composed of 4 self-attention layers, with 8 attention heads. The output representation of the “CLS” token is used as the global embedding of the implicit representation.

The RL agent

The agent is trained with RL, more precisely Proximal Policy Optimization (PPO) for 70M steps. The inner training loops of the implicit representations are supervised (red arrows in the figure below) and occur at each time step in the forward pass, whereas the RL-based outer training loop of the agent occur after N acting steps (black arrows in the figure below).

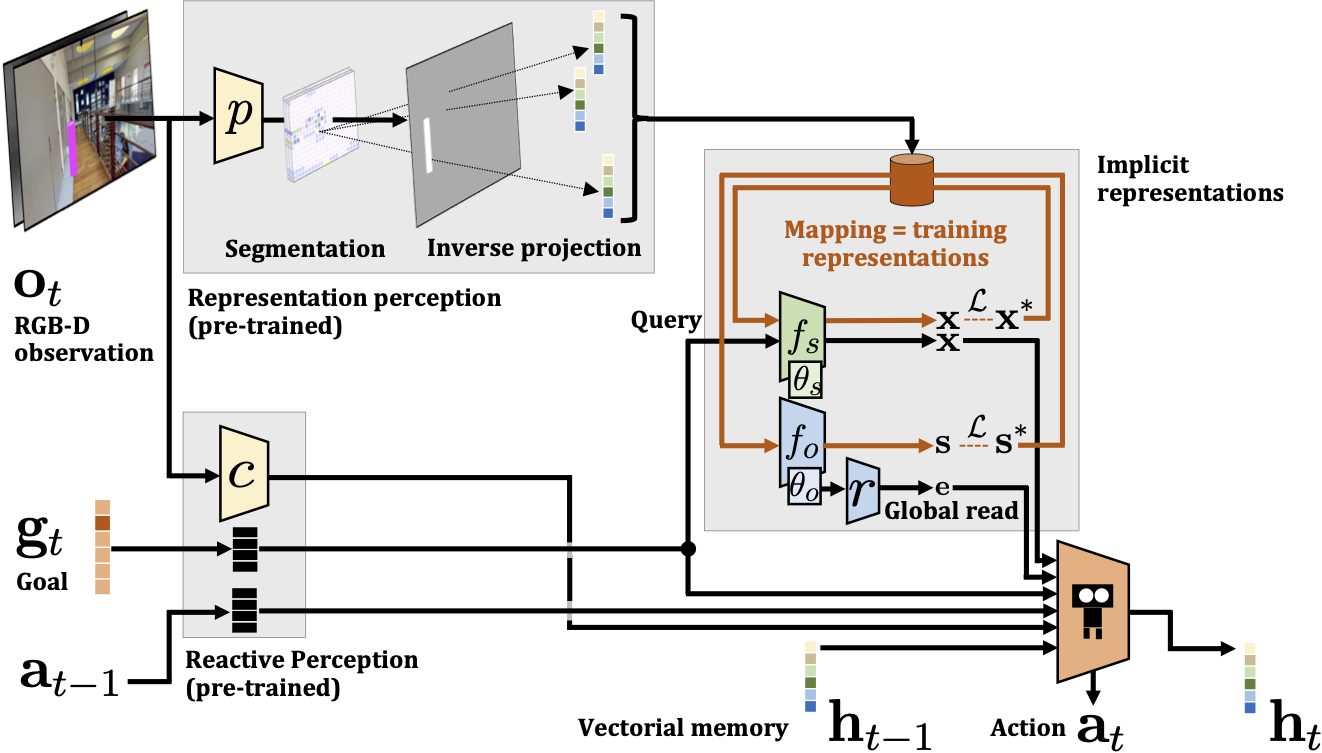
Given representations \(f_s\) and \(f_o\), a single forward pass of the agent at time step \(t\) and for a goal \(g_t\) involves reading the representations and providing the input to the policy. The current RGB-D observation \(o_t\) is also encoded by the convolutional network \(c\) (different from the projection module \(p\) used to generate samples for training the Semantic Finder). Previous action \(a_{t-1}\) and current goal \(g_t\) are passed through embedding layers, named \(L(.)\) in the following equations. These different outputs are fed to the policy,

\(\mathbf{x}_t = f_s(g_t;\theta_{s,t})\),

\(\mathbf{e}_t = r(\theta_{o,t};\theta_r)\),

\(\mathbf{c}_t = c(o_t; \theta_{c})\),

\(\mathbf{h}_t = GRU(\mathbf{h}_{t-1}, \mathbf{x}_t, u_t, \mathbf{e}_t, L(a_{t-1}), L(g_t), \mathbf{c}_t; \theta_{G})\),

\(a_t = \pi(\mathbf{h}_t;\theta_{\pi})\),

where we added indices \(\cdot_t\) to relevant variables to indicate time. Please note that the trainable parameters \(\theta_{s,t}\) and \(\theta_{o,t}\) of the two implicit representations are time dependent, as they depend on the observed scene and are updated dynamically, whereas the parameters of the policy \(\pi\) and the global reader \(r\) are not. Here, GRU corresponds to the update equations of a GRU network, where we omitted gates for ease of notation. The notation \(a_t=\pi(.)\) predicting action \(a_t\) is also a simplification, as we train the agent with PPO.

Results

To keep compute requirements limited and decrease sample complexity, in some experiments (see paper for more details) we do not train the full agent from scratch, in particular since the early stages of training are spent on learning basic interactions. We decompose training into three phases: 0−30M steps (no implicit representations, i.e. all entries to the agent related to \(f_s\) and \(f_o\) are set to 0); 30M−50M steps (training includes the Semantic Finder \(f_s\)) and finally 50M−70M steps (full model). This 3-steps approach is denoted as curriculum.

Comparison with baselines – with curriculum

As can be seen below, our method outperforms the different competing representations when trained with the curriculum scheme. We make sure that all three methods are completely comparable (by pre-training all encoders in the same way, please see paper for more details).

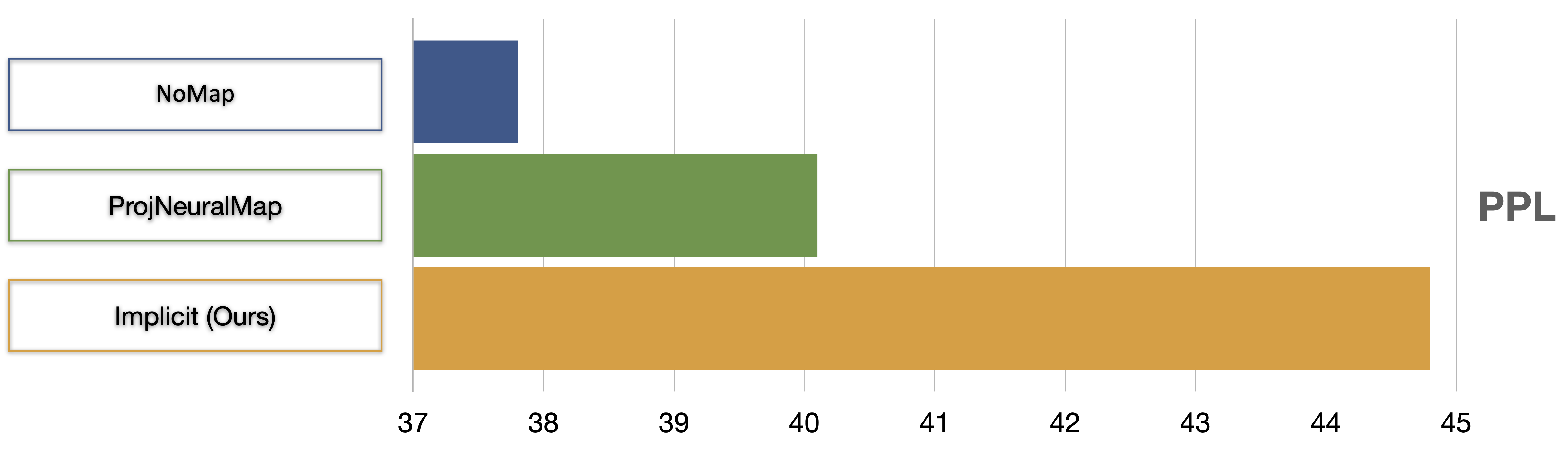
Comparison with SOTA – without curriculum

Results below show that when training with both implicit representations available to the agent at the beginning (no curriculum) and even without any pre-training of encoders, our method outperforms the previous state-of-the-art method.